Activation Functions Neural Networks

Activations functions are widely used in almost every type of Neural Networks. Feed-forward neural network, Convolutional Neural Networks and Recurrent Neural Networks use activation functions.

There are a lot of different activation functions that could be used for different purposes.

An activation function is used to separate active and inactive neurons depending on a rule or function. Depending on their status they will modify their values or not.

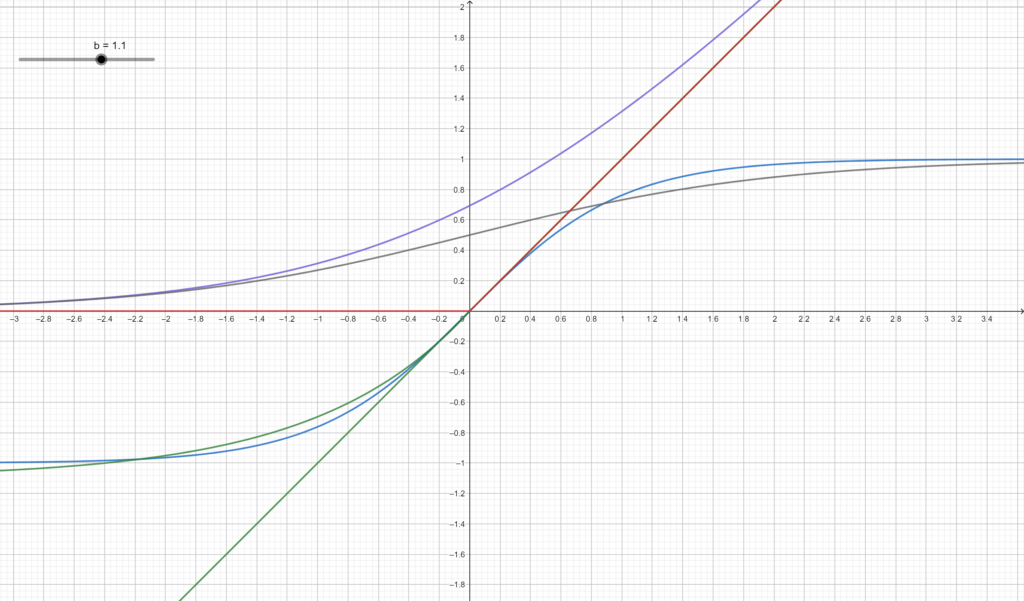
We will see a wide range of activation functions:

• Identity
• Binary Step
• Logistic (Soft Step)
• Hyperbolic Tangent
• ReLU
• ELU
• SoftPlus
• SoftMax

IDENTITY

This activation function will not produce any change to the input value. The output will be the same.

$$f(x)=x$$

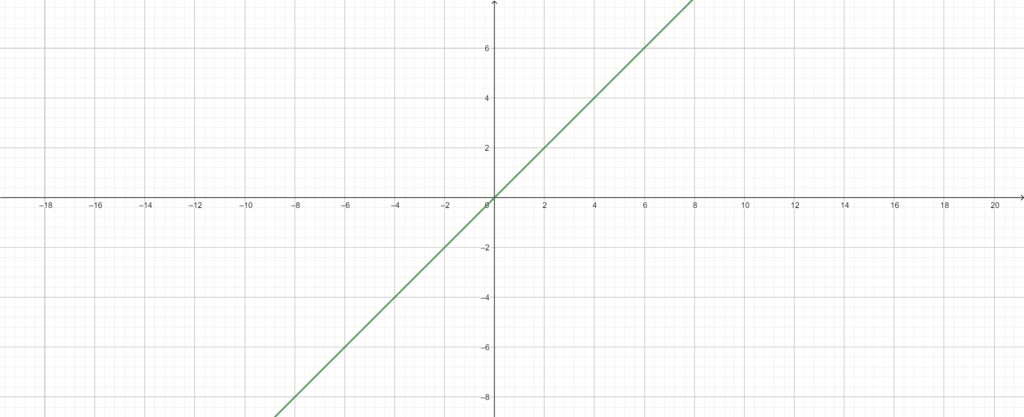
The derivative of the identity is:

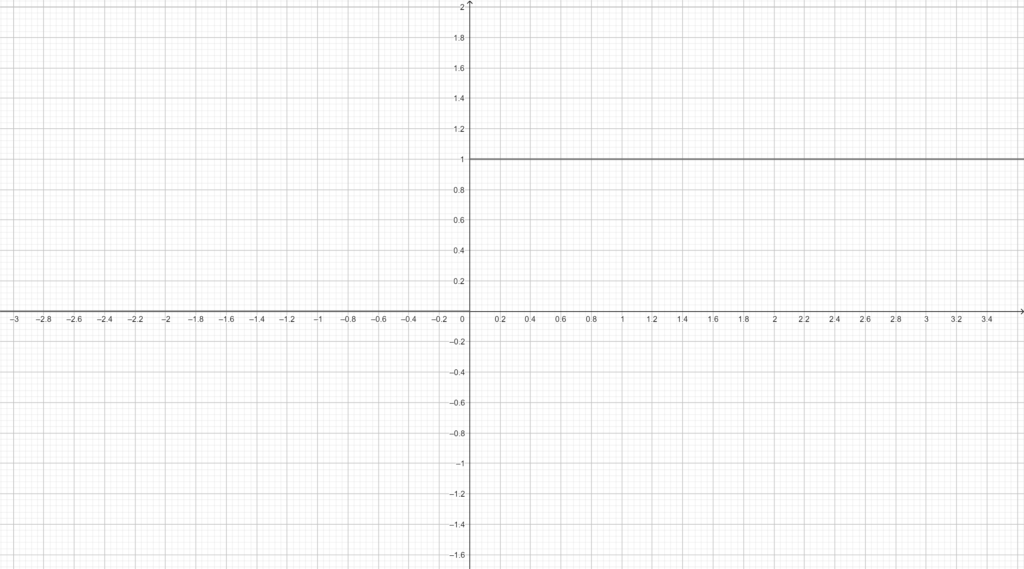
$$f'(x)=1$$

BINARY STEP

It’s a simple fragmented function.

$$f(x)= \left\{ \begin{array}{lcc}
           0 &   if & x < 0 \\
           \\ 1 &  if  & x \geq 0

             \end{array}
\right.$$

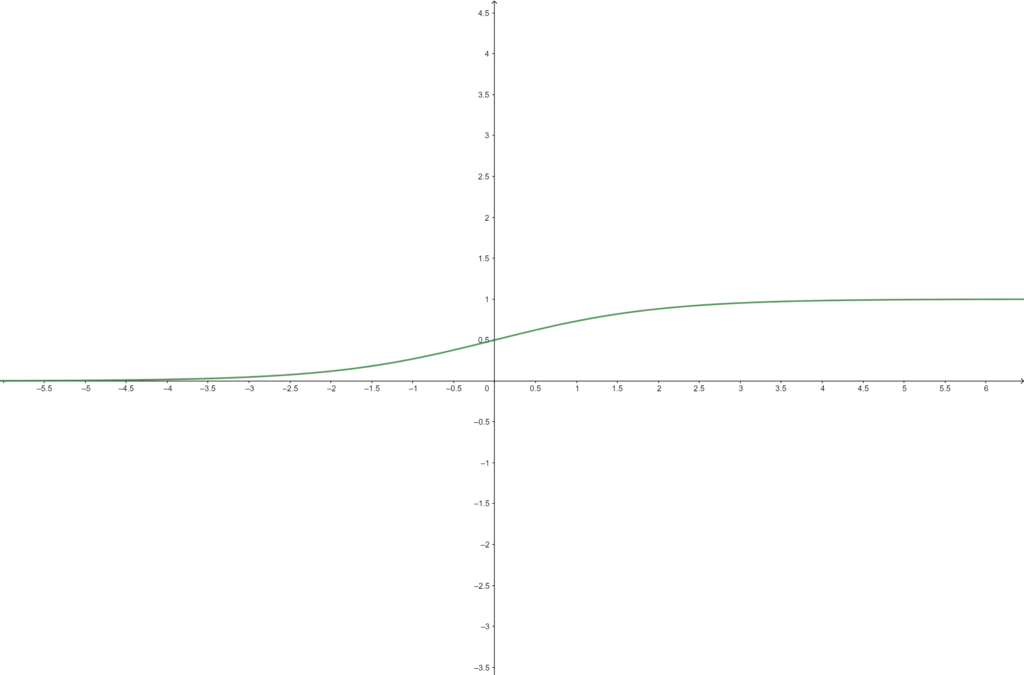
LOGISTIC

This function will be a step function but with an inferior and superior limit. This function is widely used for Feed-Forward Neural Networks

$$f(x)=\frac{1}{1+e^{-x}}$$

The derivative of the logistic function is:

$$f'(x)=f(x)(1-f(x))$$

HYPERBOLIC TANGENT

It’s very similar to the logistic function but it will tend to -1 in the $-\infty$ and to 1 in $\infty$ .

$$f(x)=\frac{2}{1+e^{-2x}}-1$$

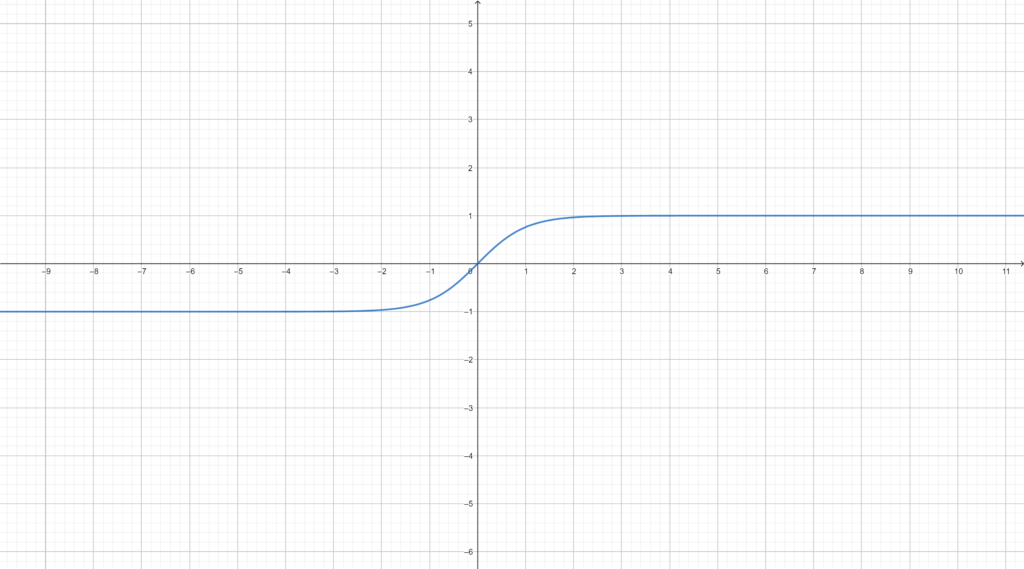
The derivative of the hyperbolic tangent is:

$$f'(x)=1-f(x)^2 $$

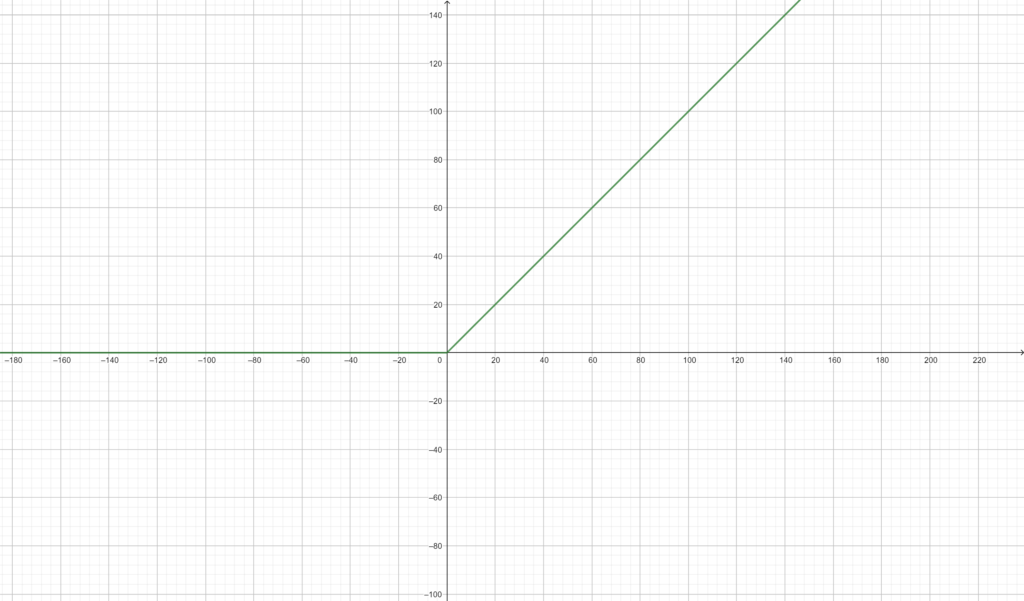
ReLU (Rectifier Linear Unit)

This is used almost every network. In the negative X axis the result will be 0 and in the right positive X axis the value will be mantained

$$f(x)= \left\{ \begin{array}{lcc}
           0 &   if & x < 0 \\
           \\ x &  if  & x \geq 0
         
             \end{array}
 \right. $$

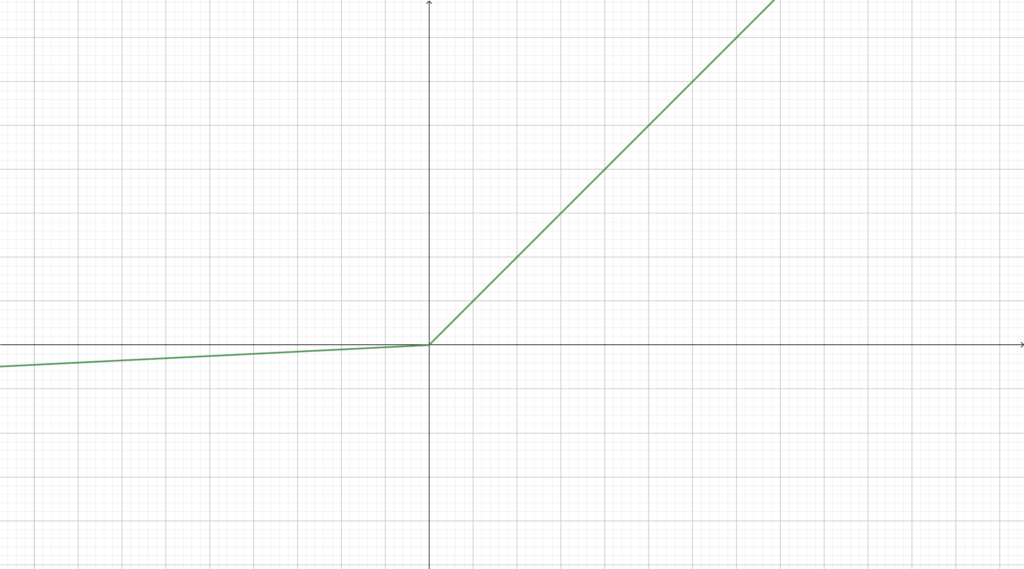
We have also one variant of this function called PReLU:

$$f(x)= \left\{ \begin{array}{lcc}
            \alpha x &   if & x < 0 \\
           \\ x &  if  & x \geq 0

             \end{array}
 \right.$$

Where $\alpha$ is a parameter to change the slope of the function

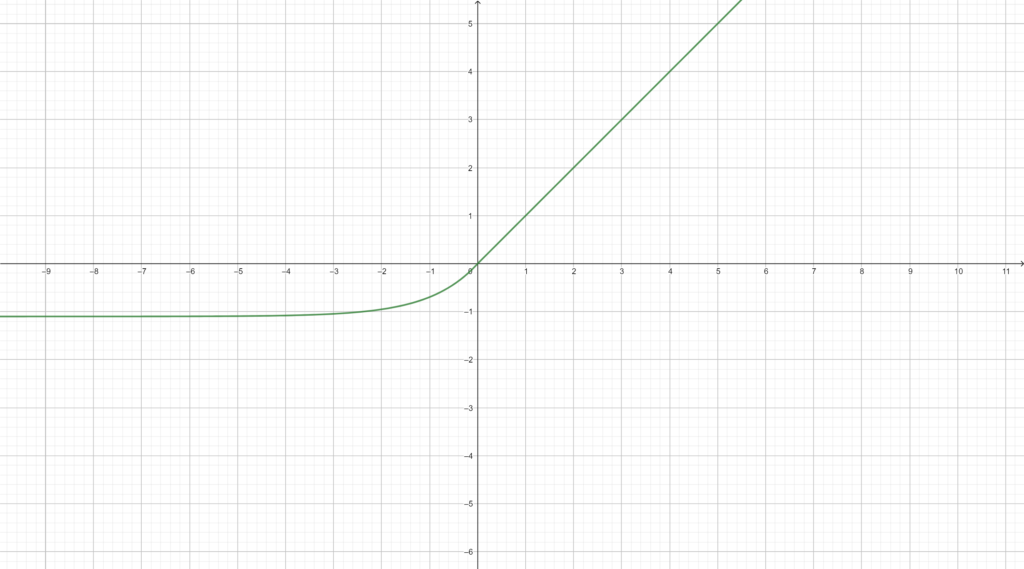
ELU (Exponential Linear Unit)

Similar to ReLU but with an exponential curve in the negative X axis.

$$f(x)= \left\{ \begin{array}{lcc}
           \alpha(e^x-1) &   if & x < 0 \\
           \\ x &  if  & x \geq 0

             \end{array}
 \right. $$

Where $\alpha$ is a parameter to edit the curve. It’s recommended a value similar to 1

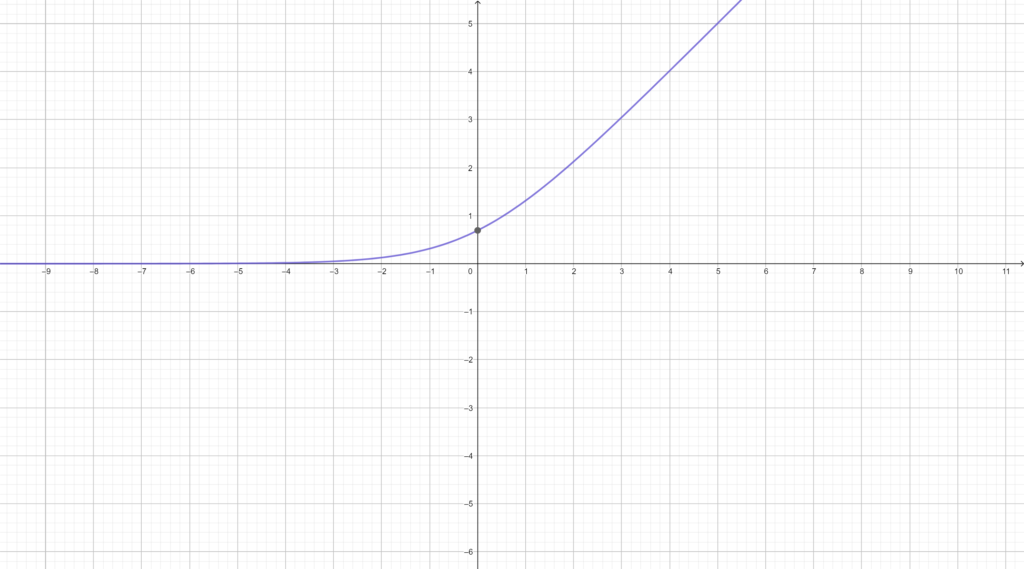
SOFTPLUS

In this function the Y value always increases.

$$f(x)=\log_e{(1+e^x)}$$

SOFTMAX

Finally we have the softmax function that is mainly used for the output layers specially in the Convolutional Neural Network.

It’s explained in the Convolutional Neural Network tutorial in the Output layer section.

To get more information about activation functions I recommend this tutorial: https://towardsdatascience.com/activation-functions-neural-networks-1cbd9f8d91d6