
Optical Physics 3D Simulation
Optical physics is the fundamental study of the light with the media. In this simulation you will see how the light in a very low speed reflects and reflacts with different media.
In the video you can watch how does white light reflects with contact glass. Also it can be refracted and disperse the white colors in the rest of the colours. This is because the waves lengths of each color are different and the refraction angle depends on this. This is explained in the presentation. The refraction is defined by the Snell Law.
In the simulation we can appreciates 3 different physics phenomenas:
Introduction to physical optics
In science, physical optics study how the light behaves depending considering its movement.
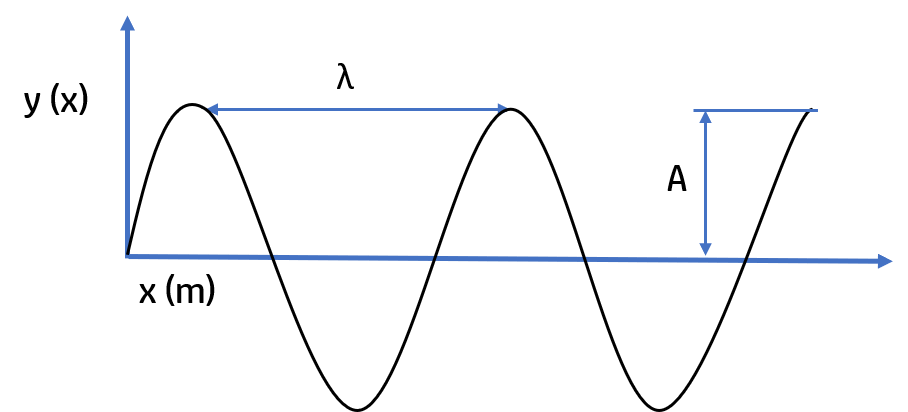
A wave is a disturbance that transfers energy through matter and space
We can calculate the propagation speed of a light ray with this formula:
$$v=\frac{\lambda}{T}=\lambda \cdot f $$
To calculate the energy of the wave we will use the constant of Plank $h$:
$$E=h \cdot f $$
Where $\lambda$ is the wave length and $f$ is the frequency. The period $T$ is inversively proportional to $f$.
In the case where the media is the vacuum, the speed will be the speed of light $c$ that is aproximately 300.000 km/s
In that high speeds the movement on the y axis of the wave is inappreciable.
However we will see the formula of the position in the $y$ axis of the wave:
$$y(x,t) = Asin(\omega t -kx+ \varphi_0)$$
Where $A$ is the amplitude of the wave, $k$ is the wave number.
$$k=\frac{2\pi}{\lambda}$$
The propagation on the X axis movement is a uniform movement
$$ x=x_0+vt$$
Reflexion
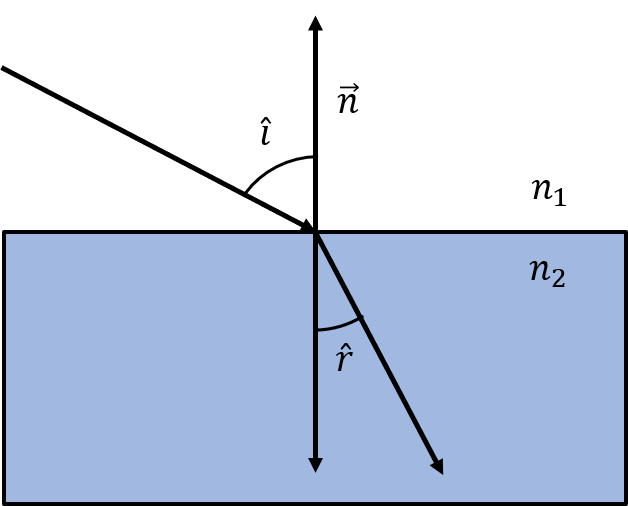
Every light ray will be reflected when it change from one media to another. The angle of reflexion will be the same with repect to the normal vector of the surface that separate the two different media.

The reflected direction will be in the same plane of the incident direction and will have the same angle with the normal vector in a 3D environment. They reflexion will always appear independently of the angle of incidence.
Refraction
The refraction is another phenomena of the light speed between two different media where the light travel with different speeds.
We will define the indice of refraction $n$ that will be an adimensional proportion relative to the speed of light.
$$n=\frac{c}{v}$$
The angle of refraction is ruled by the Snell Law where:
$$n_1sin(i)=n_2sin(r)$$
There are some incident angles where we wouldn’t have refraction. We can calculate the limit angle that is when the vector forms 90 degrees with the normal. Then if the incident angle is higher than the limit angle there would not be refreacted angle because the arcsin will be higher than one that would not have solution.
$$l=arcsin(\frac{n_2}{n_1})$$
In a two dimensional environment the refracted vector will be calculated easily because we can get the vector with trigonometrical operations. However if we do it in a 3D environment, it will be more complex.
To calculate the 3D vector we will have to do the following equation:
$$\vec{t}=\sqrt{1-\left(\frac{n_1}{n_2}\right)^2[1-(\vec{n}\cdot\vec{i})^2]}\vec{n} + \frac{n1}{n2}[\vec{i}-(\vec{n}\cdot\vec{i})\vec{n}]$$
The demonstration of this equation can be obtained here: 3D vectorial refraction.
Dispersion
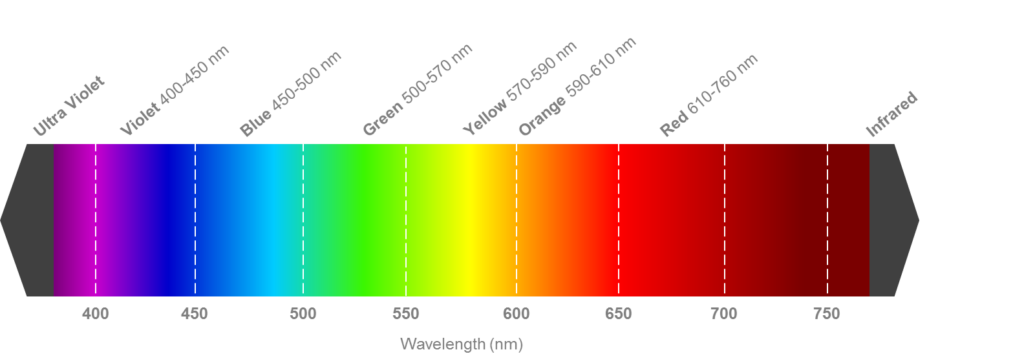
White light contains all the colors. When white light is refracted, the colors are dispersed because they have different wave lengths.
Consequently the refracted indices of refraction will differ and also the angles of refraction. This is why the white light is dispersed.
The wavelengths of the colors are in the range of 400nm and 800nm.
Here you can see the explanation video of the 3D simulation calculations and dispersion, reflexion and refraction:
If you want to look up the presentation in the explanation video you can watch it here:
[embeddoc url=”https://tutorials.retopall.com/wp-content/uploads/2019/02/Optic.pptx” download=”all” viewer=”microsoft”]The simulation it’s written in C# using Unity 3D. The full project download is available for the Programming Members.
If you are a programming member that have bought the programming tier you will see the files here:
[pms-restrict subscription_plans=”179″]
[/pms-restrict]
